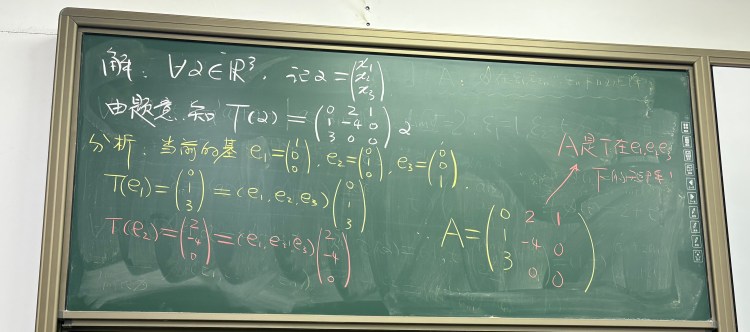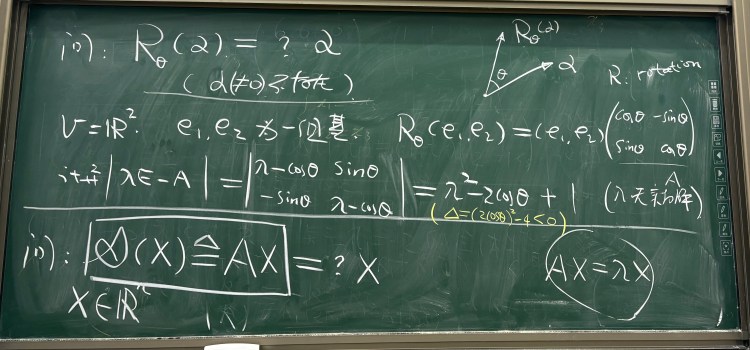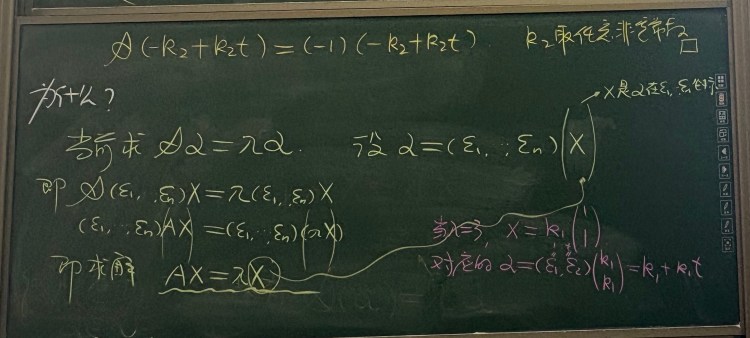— 为人工智能本科专业开设
自2023年秋起,这门课程为人工智能本科专业首次开设。今年是课程开设第3年。
选课学生名单
| 2021317220328* | 袁新娜 |
| 2022317220409* | 刘勇 |
| 2022317220611* | 左弘泽 |
| 2021317220404 | 韩林玉 |
| 2021317220619 | 王钰 |
| 2023307210412 | 谢新宇 |
| 2023317220103 | 储启启 |
| 2023317220107 | 朱锦铭 |
| 2023317220113 | 李乐童 |
| 2023317220118 | 王彪 |
| 2023317220125 | 黄晓悦 |
| 2023317220128 | 周晓慧 |
| 2023317220212 | 王振华 |
| 2023317220215 | 张楠 |
| 2023317220226 | 孙哲妍 |
| 2023317220229 | 许可凡 |
| 2023317220301 | 李荣臻 |
| 2023317220303 | 张瑛豪 |
| 2023317220405 | 沈浩 |
| 2023317220416 | 顾昊 |
| 2023317220420 | 李若冰 |
| 2023317220421 | 邵诗怡 |
| 2023317220503 | 陈浩 |
| 2023317220516 | 刘畅 |
| 2023317220609 | 陈思远 |
| 2023317220704 | 费翔 |
| 2023317220719 | 彭思瑞 |
| 2023317220724 | 刘颖霖 |
| 2021317220213 | 石富豪 |
| 2022317220503 | 容温礼 |
| 2023306220306 | 郭炼 |
| 2023307220402 | 黄泰 |
| 2023317220115 | 廖俊泰 |
| 2023317220220 | 蒋志恩 |
| 2023317220309 | 刘博 |
| 2023317220314 | 杨竣森 |
| 2023317220322 | 陕雯渊 |
| 2023317220324 | 严云佳 |
| 2023317220325 | 高雨平 |
| 2023317220404 | 陈佳伸 |
| 2023317220415 | 冉乾坤 |
| 2023317220507 | 严浩泽 |
| 2023317220514 | 陈俊豪 |
| 2023317220519 | 李泽坤 |
| 2023317220522 | 王紫烜 |
| 2023317220605 | 龚毅 |
| 2023317220606 | 汪奇 |
| 2023317220610 | 彭传钰 |
| 2023317220612 | 游自豪 |
| 2023317220702 | 任佳鹏 |
| 2023317220705 | 阮怀明 |
| 2023317220727 | 陈乐萦 |
| 2023317220728 | 杨雯 |
More about matrix!
欢迎选课
为什么要选这门课程?
本课程讲述矩阵代数中的一些基本问题和方法,通过课程学习,讲述空间、变换、范数、矩阵分析等近现代数学元素对象和相关理论方法。借由课程学习,助学生理解代数语言下对算法模型的一般性刻画,初步了解矩阵代数在最优化、数据挖掘、机器学习等领域的应用结合,为人工智能专业高年级同学后续从事科学研究和工程实践打好理论基础。
Discover The Syllabuse
发现课程
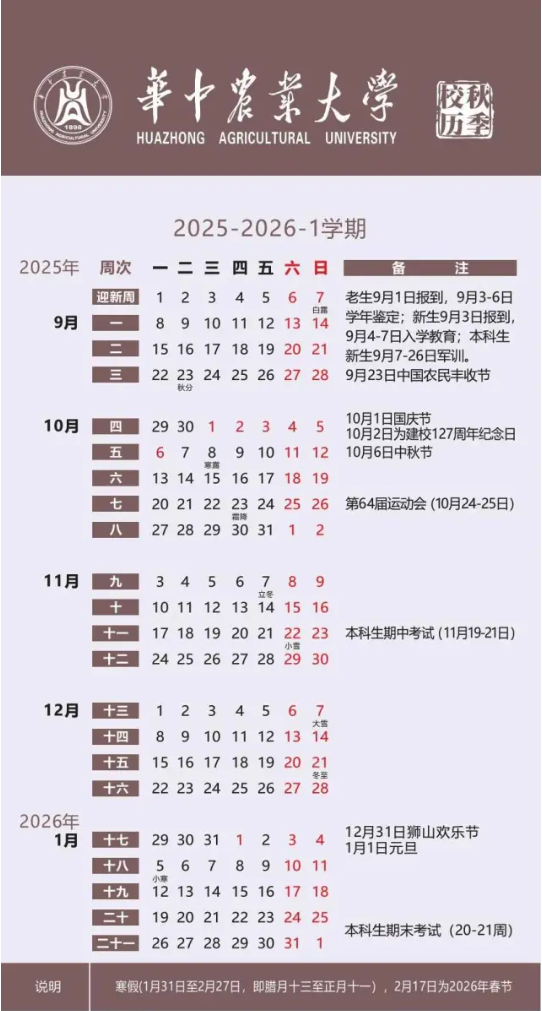
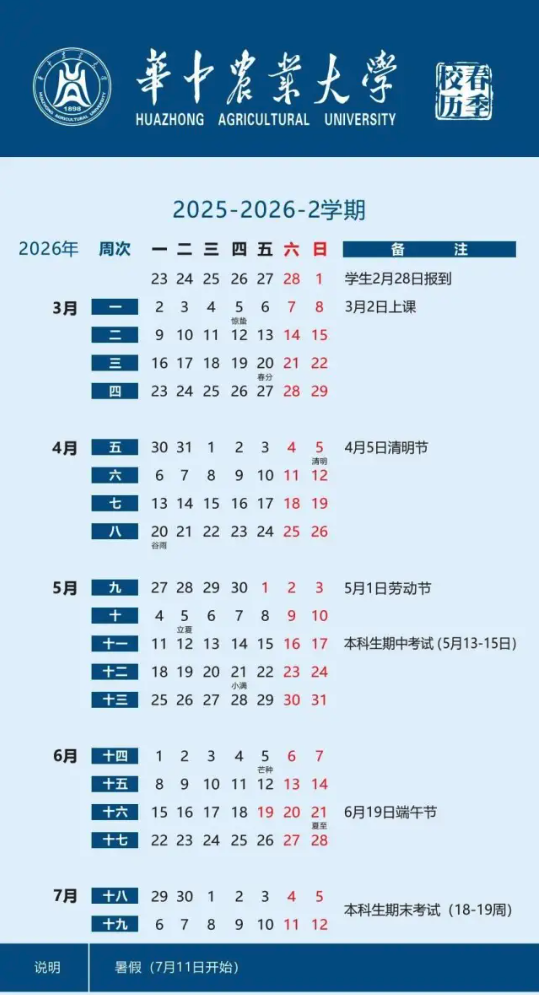
一、日程安排
| 日期 | 内容 (§x.x.x为西北工业大学《矩阵论》对应章节编号 ) |
| 25, Nov | ▩ Ch1.《线性空间与线性变换》 — — 集合与映射 (§1.1.1 ) — — 线性空间及其性质 (§1.1.2) |
| 28, Nov | ▩ Ch1.《线性空间与线性变换》 — — 线性空间的基与坐标 (§1.1.3) — — 专题1《从极大无关组,到基础解系,到空间的基向量》 |
| 2, Dec | ▩ Ch1.《线性空间与线性变换》 — — 基变换与坐标变换 (§1.1.4) |
| 5, Dec | ▩ Ch1.《线性空间与线性变换》 — — 线性子空间 (§1.1.5) — — 子空间的交与和 (§1.1.6) |
| 9, Dec | ▩ Ch1.《线性空间与线性变换》 –— — 线性变换及其运算 (§1.2.1) |
| 12, Dec | ▩ Ch1.《线性空间与线性变换》 — — 线性变换的矩阵表示 (§1.2.2) — — 专题2《从R^n到一般线性空间,从矩阵A到变换A》 ——“Rn之于一般线性空间,基之于空间,矩阵之于变换。” |
| 16, Dec | ▩ Ch1.《线性空间与线性变换》(学生笔记) — — 特征值与特征向量 (§1.2.3) |
| 19, Dec | ▩ 习题课 (《线性空间与线性变化》Slides) |
| 23, Dec | 专题3《数学模型中的矩阵表示和微分计算》(《矩阵微分》AI讲义) ——“数学模型和最优化问题求解” |
| 26, Dec | 专题4《优化问题中的范数正则项》 (《专题:矩阵论和算法》Slides) ——“用代数语言刻画模型,正则项的范数选取,优化问题的约束条件。“ — — 几种常见的矩阵范数 (§2.2.2) |
| 30, Dec | ▩ Ch2. 《范数理论及其应用》 — — 向量范数(§2.1) |
| 4, Jan | ▩ Ch2. 《范数理论及其应用》(《范数理论》Slides) — — 矩阵范数 (§2.2) |
| 6, Jan | ▩ Ch3. 《矩阵分析及其应用》 — — 矩阵函数 (§3.3) — — 矩阵的微分 (§3.4 ) |
| 9, Jan | ▩ Ch3. 《矩阵分析及其应用》(《矩阵函数和矩阵微分》Slides) — — 矩阵的微分 (§3.4 ) |
| 13, Jan | ▩ Ch4. 《矩阵分解》(《奇异值分解》Slides) — — 矩阵的正交对角分解与奇异值分解 (§4) — — 专题5《矩阵分解的应用》 |
| 16, Jan | ▩ 学期总结 |
二、课程考核
- 平时 50%
- 期末考试 50%
三、课程讨论进程
♥ 课堂掠影
♥ 线代考研习题
♥ 空间的基
♥ 子空间
♥ 生成子空间的基与维数
♥ 线性变换的定义
♥ 线性变换的矩阵
♥ 特征值与特征向量

♥ 线性空间与变换习题讲解
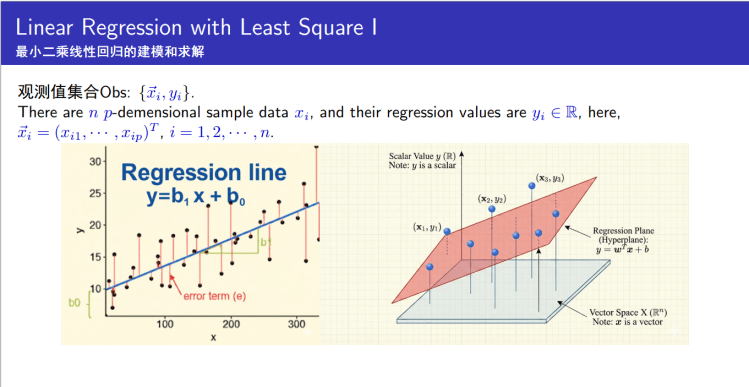
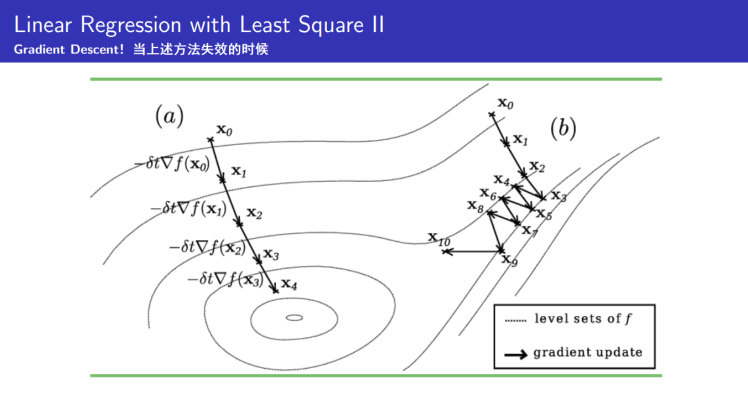
♥ 线性回归中的矩阵计算
(课件:《线性回归与正则项》)
(AI讲义:《线性回归、岭回归与LASSO回归》)
♥ 特征值与特征向量
Course Resources and External Links
课程资源和外部链接
四、推荐文献-课外阅读
☁ 1. 扩展阅读——矩阵函数在建模中的典型应用——以一篇因果推断论文为例。(矩阵函数用以统计通路数量——请联系《离散数学》图论部分相关结论)
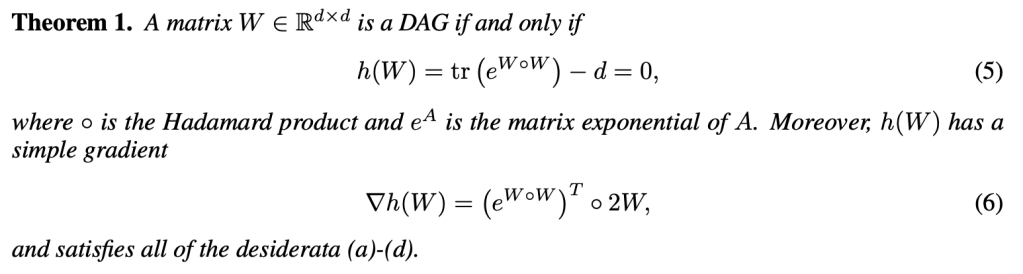
Zheng, Xun, et al. “DAGs with no tears: Continuous optimization for structure learning.” Advances in neural information processing systems 31 (2018). (Link)
☁ 2. 扩展阅读——矩阵分解论文。Daniel D. Lee & H. Sebastian Seung (1999). “Learning the parts of objects by non-negative matrix factorization”. Nature. 401 (6755): 788–791. (Link)
Find us!
找到我们!
课后答疑
办公室: 一综B417
Course for BioNLP
学科交叉,融会贯通,学好BioNLP.
Course Hours
See jw.hzau.edu.cn
Office
C610, Yifu bldg
Contact me
xiajingbo.math@gmail.com