Data Mining 2024 Spring

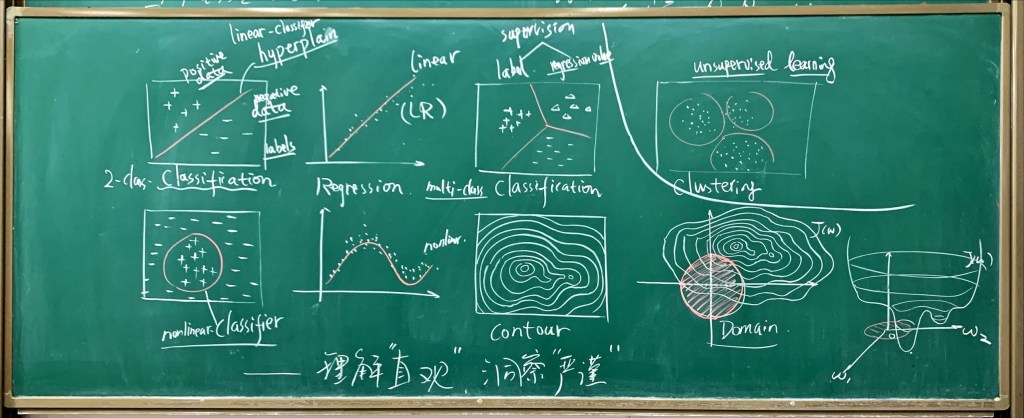
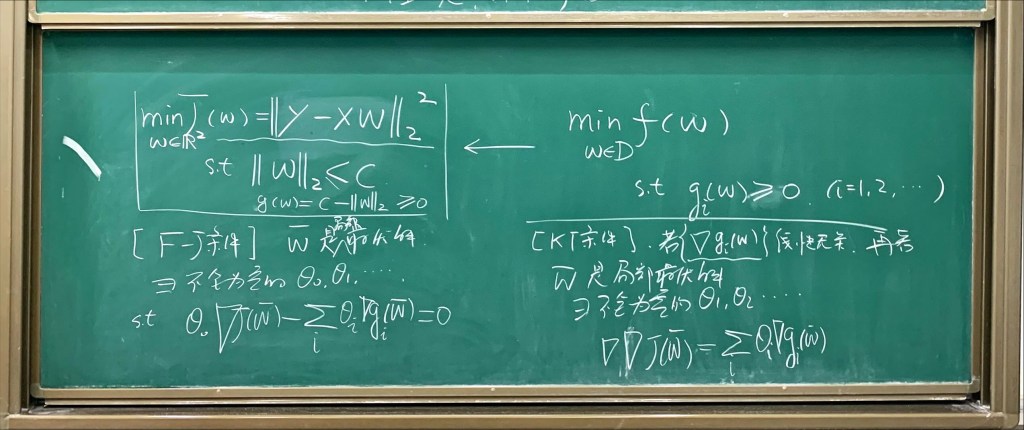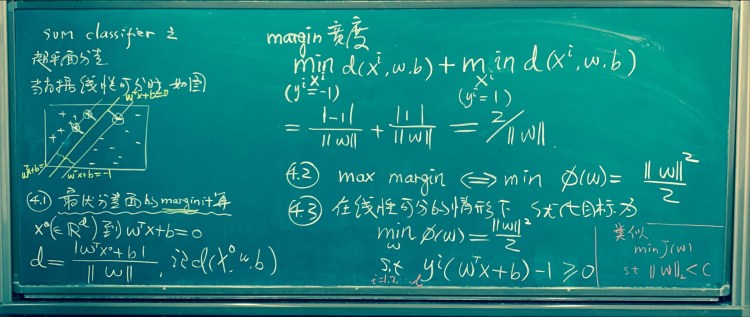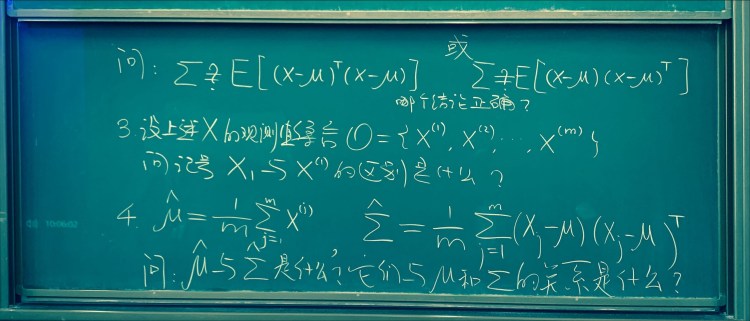— A Course for Graduates in HZAU.

_{缘起：“这门课自2017年开始每年秋季开设，（历年选课人数：17，36，36，68，67，67）；自2024年起调整为春季讲授，今年选课人数19人；授课地点A410，最后一次课在襄阳书院。”}

_{问：“为什么在LLM时代仍然要学习算法理论，尤其是背后的数学原理？”}

点击展开回答

在大模型时代，虽然深度学习等大规模模型取得了显著的成功，但学习算法理论和背后的数学原理仍然具有重要的价值。以下是一些原因：

理解模型的原理： 深刻理解算法理论和数学原理可以帮助你更好地理解模型的工作原理。这对于调试、优化和设计新模型都是至关重要的。
问题理解与定制模型： 对算法理论的深刻理解使你能够更好地理解不同问题的特性，并有能力为特定问题选择、设计和定制模型。
解释模型预测： 理解数学原理使你能够更好地解释模型的预测结果，推导模型对输入的敏感性，并提供对模型行为的洞察。
调参和优化： 对算法背后的数学原理有深刻理解的人更容易调整和优化模型，以提高性能、减少过拟合等。
处理非标准问题： 对算法理论和数学原理的了解使你能够更自如地处理非标准或特殊类型的问题，而不仅仅依赖于黑盒模型。
创新和研究： 在大规模模型之外的研究和创新通常需要对算法和数学的深入理解。新的理论和方法往往是由对基本原理的深刻理解产生的。
避免误用和陷阱： 对算法背后的原理的理解可以帮助你避免在使用模型时常见的误用和陷阱，确保模型的有效性和可解释性。
适应新技术： 深刻理解算法原理和数学基础使你更容易适应新的技术和方法。这种适应能力在快速发展的领域中尤为重要。

虽然大规模模型在许多任务上取得了惊人的成功，但对算法和数学原理的理解依然是从事机器学习和人工智能领域的从业者所需的核心能力之一。深入理解背后的原理可以使从业者在实际应用中更具有创造性和灵活性。

一、课程内容和周次安排

26,Feb	▩ Preface ▩ 《Introduction to This Course》 ▩ 《入手数据挖掘算法，朴素贝叶斯》【1】
28,Feb	▩ 最优化基础——《最优化理论与算法之 1，引言》【2】
04,Mar	▩ (Quiz 1) 考核点：算法公式推导 ▩ 最优化基础——《最优化理论与算法之 1，引言》【2】
06,Mar	▩ 经典算法——《线性回归，LOSS 函数与范数》【3】 ▩ 最优化基础——《最优化理论与算法之 7，最优性条件》【2】
11,Mar	▩ 最优化基础——《最优化理论与算法之 7，最优性条件》【2】 ▩ 【专题】：《线性回归优化目标的KT条件》
18,Mar	▩ 最优化基础——《最优化理论与算法之 7，最优性条件》【2】 ▩ 经典算法——《SVM/支撑向量机》【1,3】
25,Mar	▩ 经典算法——《SVM/支撑向量机》【1,3】
01,Apr	▩ (Quiz 2) 考核点：案例建模和模型选择 ▩【专题】：《分类和回归算法的总结归纳》（学生汇报） ▩ 经典算法——《从SVM到SVR，从分类到回归》【1,3】
08,Apr	▩【专题】：《数据的低维表示》 ▩ 经典算法——《从 SVD 到 PCA》【3】
15,Apr	▩ 经典算法——《神经网络，从传统到摩登》【1】 ▩【专题】：《Auto-encoder、Word2Vec、和表示学习的兴起》
22,Apr	▩ 经典算法——《硬/软聚类，单高斯模型》【1,3】 ▩ 进阶算法——《第一个隐变量模型：混合高斯模型》【1】
29,Apr	▩ 进阶算法——《EM 算法，如何求解混合高斯模型》【1】
06,May	▩ (Quiz 3) 考核点：算法细节和创新思维 ▩ 【专题】：《基于隐变量的一般贝叶斯方法和EM算法的实质》
13,May	▩ 进阶算法——《第二个隐变量模型：LDA主题模型》【3】 ▩ 进阶算法——《LDA主题模型和（EM框架下的）变分推断算法》
20,May	▩ 进阶算法——《第三个隐变量模型：VAE/变分自编码机》
03,Jun (襄阳)	▩ 进阶算法——《漫谈流行，神经网络、强化学习、VAE 和 GAN》 ▩ 论文研讨——VAE, Kingma and Weiling, 2013(Paper Link) ▩ (Term Exam)-6月10日，19:00，4教A408

1718017200

days

hours minutes seconds

until

(Term Exam)-6月10日，19:00，4教A408

_{参考教材：}

_{【1】李航《统计学习方法》清华大学出版社}

_【2】_{陈宝林《最优化理论与算法》清华大学出版社}

_{【3】周志华《机器学习》清华大学出版社}

Course Note Available upon Request:

Link to the request page.

二、考核方式:

3+1: 平时测验(×3) + 期末考查(×1)

注：Quiz的设置目的包括算法基础摸底、过程学习督促，请勿为此困扰。

. /_/ .可选项：

.( o.o ).期末可提交课程笔记

. > ^ < .期末可提交算法心得(仅限课程所讲授算法)

三、课堂进程：

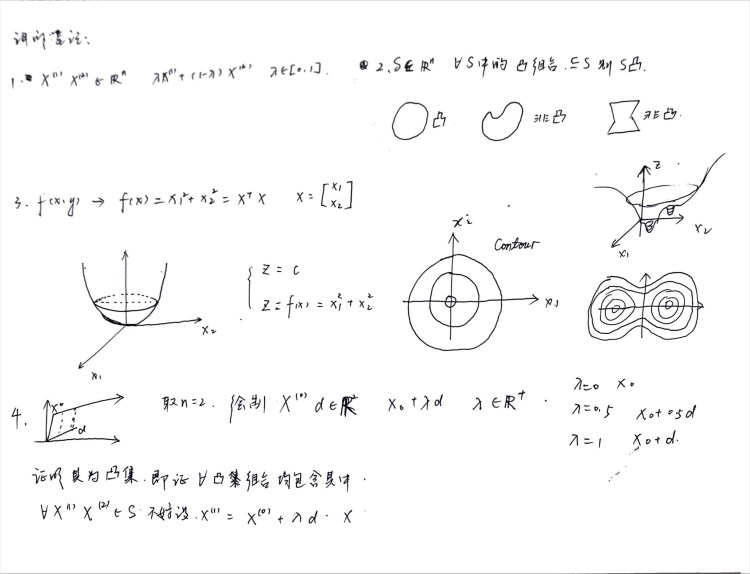
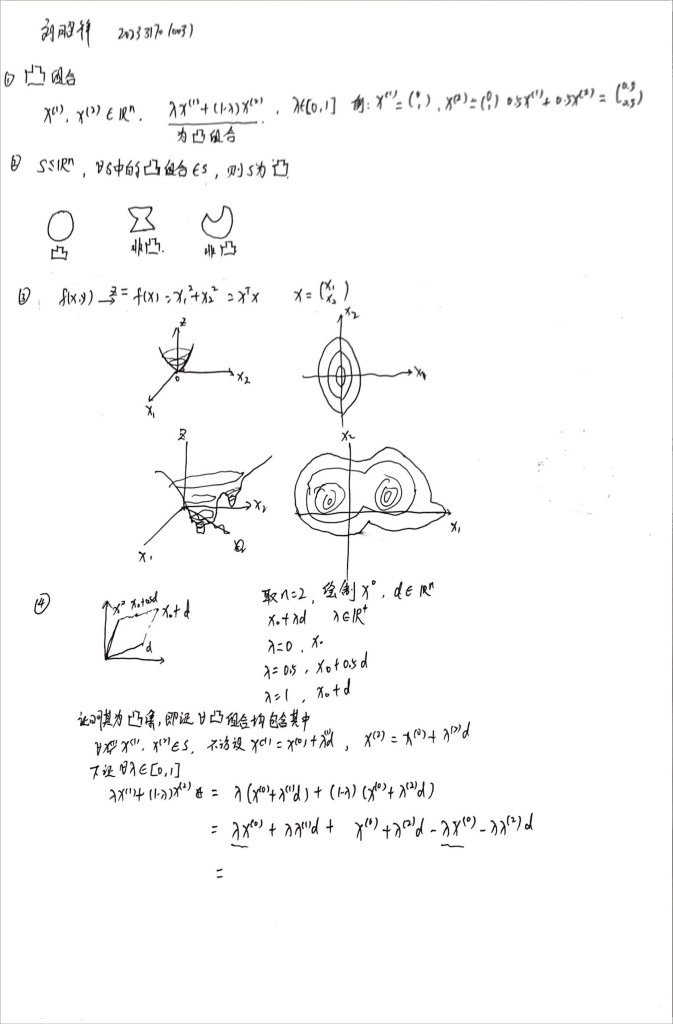
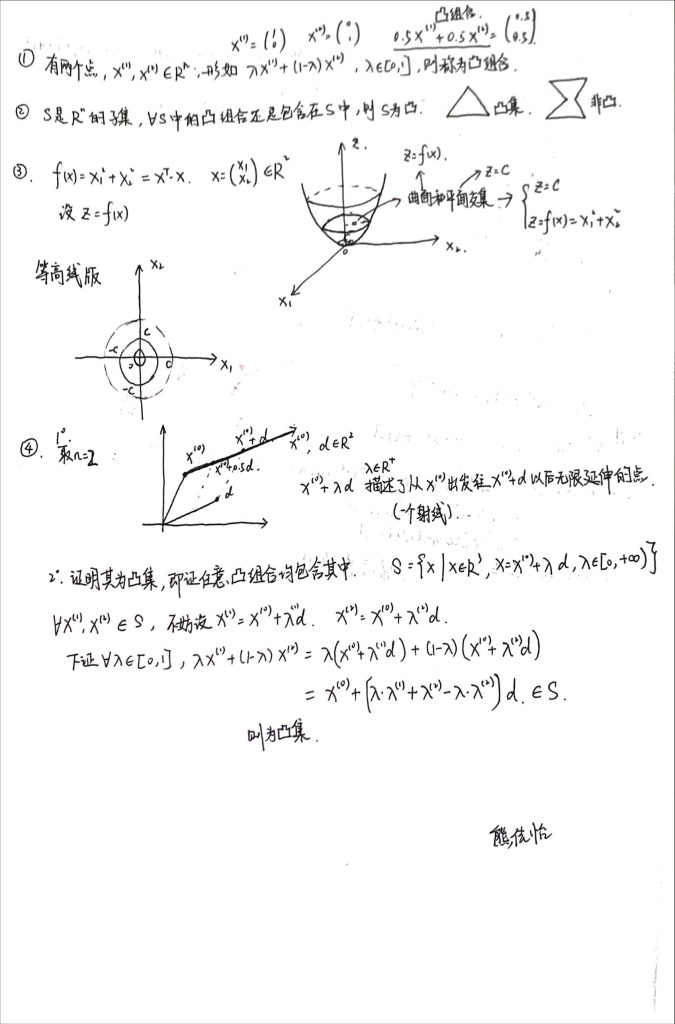
《凸集与分离定理》-讲义摘拍视频

Quiz 1 (Mar/2024)

《线性回归》-讲义摘拍视频

《若干总结：Loss函数、梯度下降、任务和模型》(Mar, 2024)

《最优性条件》-讲义摘拍视频

《SVM》(Mar, 2024)

《波士顿房价预测-DM任务》

分析《波士顿房价预测-DM任务》https://www.kaggle.com/c/boston-housing，回答：

简答：能否选用分类模型来解决该任务?
简答：该任务中，模型评价标准是什么？
详述：请写出使用LASSO回归求解上述问题的算法过程。（请准确使用数学符号表征问题中的数据、问题和求解过程。）

《学生讨论和材料》(Apr, 2024)

项昌鹏-KNN（K近邻算法) (Slides)
方文涛-有监督学习方法 (Slides)
石祥龙-回归与分类 (Slides)
李桂淇-Data Mining学习路线 (Slides)
宋伟-回归算法波士顿房价预测 (Slides)
肖易敏-分类和回归算法的总结归纳 (Slides)

_{（讨论材料版权归属学生个人所有，仅供学习分享。）}

《PCA的若干算法结论准备》(Apr, 2024)

《高斯混合模型Gaussian Mixture Model和EM算法》——讲义摘拍，视频

《隐变量模型和EM求解——总结》

在高斯混合模型GMM中，隐变量Z起的什么作用？请用公式回答。
一般情形下，EM算法中E步和M步分别的求解对象是什么？
在求解GMM时，EM算法的E步和M步分别是什么？请用公式回答。
在“一个轻量级的高斯混合模型求解的视频 (Victor Lavrenko, 时长：～14 min)”中，作者假定K=2，并以yellow（a）和blue（b）为例，给出了最终的迭代公式。假设K=3，增设green（c），请给出更替后的迭代公式。

《变分推断算法-理论篇》——Slides，视频